Take the Knight Tour Challenge

The earliest references are from the 9th century AD. The pattern of a Knight's path on a half-board was created by Indian poet Rudrata. I can't tell you if Rudrata solved the puzzle. But the existence of a pattern suggests that a solution had been found whether by Rudrata or some mathematicians of the era.

Not surprisingly, it was originally difficult to work out correct patterns for the tour simply by trial and error. There are literally billions of possible paths the Knight could take across the board so mathematicians were needed to make the breakthrough.

Leonhard Euler (1707-1783) devised a method for plotting a path in 1759. Others like Warnsdorff also contributed significant work on the Knight's Tour riddle.

Is this challenge just a way to kill a half hour? Just a time filler? Or is there some tangible gains to be had in trying to beat this puzzle?

I think it builds a subliminal appreciation for the scope of the Knight. The squares under the command of the Knight. The most efficient way to maneuver the Knight to get from one location to another.

You bring the Knight around the board for the second and third laps. Now as you maneuver the Knight in between the squares already touched to cover the remaining squares it will be like finding useful outposts among a forest of pieces just as you would in a real game.

No messing about, this challenge is hard. If you try to solve it yourself without the solution, good luck. Well maybe you can but if so, you might be a genius.

Now I'm not saying you won't get most of the squares, just going off the cuff. You might get 60, 61, 62 squares. But there is a narrow path, a very precise strategy. If you make even one wrong move, you can't fix it. Like an actual game, if you mess up the opening, you may last another 40 moves but ultimately you're doomed.

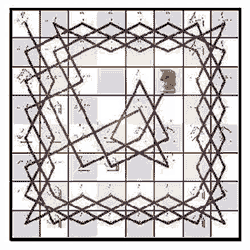
You'll have fun trying to crack the code on you're own. And like I say, if you're some kind of prodigy, maybe you might even do it. On the other hand you could just cast an eye on this image for the solution.

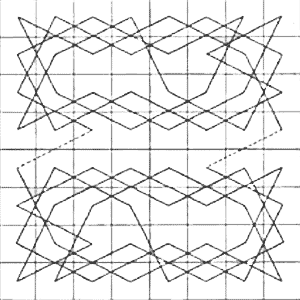
Having heard a little bit about this you may feel it's time to give it a try. There are a number of good places on the web to do so. Might I suggest for instance The Knight Tour to get you started.

The Knight's move is a perfect phenomenon for getting around the board, hitting each square once and only once. You can run around the corners, hit some squares and then hit the remainders on your return. If you do it right, you will have the perfect path even on the last lap.

These links will open in a new tab. The diagram shows one of virtually countless solutions. This is something that has sparked a wide interest and there is plenty of related material out there. I would like to point you to the definitive directory on the Knight Tour.